3. Analýza kombinačního obvodu

• Předurčení analýzy kombinačního obvodu
• Postup analýzy kombinačního obvodu na příkladu
• Sestavení pravdivostní tabulky a logické funkce na základě analýzy

---

Předurčení analýzy kombinačního obvodu

• Určení počtu a významu vstupních a výstupních proměnných analyzovaného obvodu
• Kombinační obvody jsou obvody, výstupy závisí na aktuálních hodnotách vstupů.
• Obvody se skládají z logických hradel, jako jsou AND, OR, NOT, NAND, NOR, XOR a XNOR.

Postup analýzy kombinačního obvodu na příkladu

Analýza obvodu

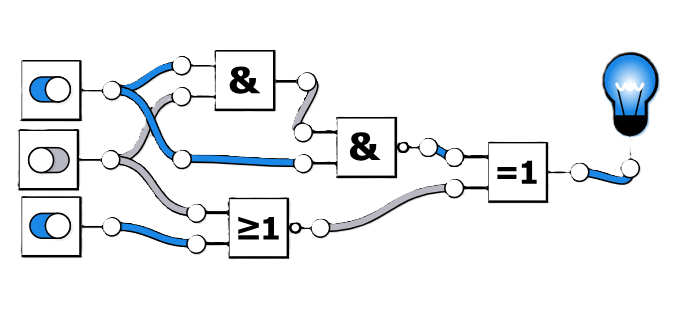
1. Identifikace výstupů a vstupů
   • Vstupy: Tři přepínače A, B, C. (Možné stavy přepnutí zapnuto (1) a (0).
   • Výstup: Žárovka Y. Žárovka může být buď svítit (1) nebo nesvítit (0).
2. Určení použitých logických členů
   • Hradlo AND (označené ”&”) - na vstupu má A a B
   • Hradlo NAND (označené ”&”) - na vstupu má výstup prvního hradla AND a C
   • Hradlo NOR (označené “≥1”) - na vstupu má B a C
   • Hradlo XOR (označené “=1”) - na vstupu má výstup druhého hradla NAND a hradla NOR
3. Zapsání výstupních funkcí Mezivýstupy:

   • $W1=A\cdot B$

   • $W2=\overline{W1\cdot C}$

   • $W3=\overline{B+C}$

   • $Y=W2\oplus W3$ Rozepsání:

     $Y=\overline{(A\cdot B\cdot C)}\oplus \overline{(B+C)}$

4. Zjednodušení logických funkcí

   1. Výchozí rovnice $Y=\overline{A\cdot B\cdot C}\oplus \overline{B+C}$

   2. Rozepsání XOR pomocí základních operací XOR můžeme rozepsat jako: $Y=(\overline{A\cdot B\cdot C}\cdot \overline{(B+C)})+((A\cdot B\cdot C)\cdot \overline{(B+C)})$

   3. Použití De Morganova zákona Podle De Morganových zákonů platí: $\overline{A\cdot B\cdot C}=\overline{A}+\overline{B}+\overline{C}$ $\overline{(B+C)}=\overline{B}\cdot \overline{C}$

      Dosadíme tyto výrazy do rovnice: $Y=((\overline{A}+\overline{B}+\overline{C})\cdot \overline{(B+C)})+((A\cdot B\cdot C)\cdot (\overline{B}\cdot \overline{C}))$

   4. Distributivní zákon Aplikujeme distributivní zákon: $(\overline{A}+\overline{B}+\overline{C})\cdot (B+C)=(\overline{A}\cdot B)+(\overline{A}\cdot C)+(\overline{B}\cdot B)+(\overline{B}\cdot C)+(\overline{C}\cdot B)+(\overline{C}\cdot C)$

      Zjednodušením, protože $\overline{B}\cdot B=0$ a $\overline{C}\cdot C=0$: Y = ($\overline{A}\cdot B)+(\overline{A}\cdot C)+(\overline{B}\cdot C)+(\overline{C}\cdot B)+(A\cdot B\cdot C)\cdot (\overline{B}\cdot \overline{C})$

   5. Zjednodušení výrazu Vzhledem k tomu, že $A\cdot B\cdot C\cdot (\overline{B}\cdot \overline{C})$ je vždy 0: $(A\cdot B\cdot C)\cdot (\overline{B}\cdot \overline{C})=0$

      Tedy dosadíme zpět: $Y=(\overline{A}\cdot B)+(\overline{A}\cdot C)+(\overline{B}\cdot C)+(\overline{C}\cdot B)$

   6. Úprava pro podobnost Upravíme výrazy $Y=(\overline{A}\cdot B)+(\overline{A}\cdot C)+(\overline{B}\cdot C)+(B\cdot \overline{C})$

   7. Zkrácení vytknutím A Zkrátíme pomocí vytknutí:

      $Y=\overline{A}(B+C)+\overline{B}C+B\overline{C}$

   • Konečná rovnice Dostaneme konečnou formu: $Y=\overline{A}(B+C)+\overline{B}C+B\overline{C}$
5. Vytvoření pravdivostní tabulky
   • Pravdivostní tabulka bude mít 2^3 = 8 řádků, protože máme tři vstupy
   • Vytvoření dosazováním do logické funkce nebo fyzickým testováním

$A$	$B$	$C$	$W1(A\cdot B)$	$W2(\overline{A\cdot B\cdot C})$	$W3\overline{(B+C)}$	$Y(W2\oplus W3)$
0	0	0	0	1	1	0
0	0	1	0	1	0	1
0	1	0	0	1	0	1
0	1	1	0	1	0	1
1	0	0	0	1	1	0
1	0	1	0	1	0	1
1	1	0	1	1	0	1
1	1	1	1	0	0	0

6. Ověření správnosti analýzy
   • Na základě pravdivostní tabulky vidíme následující chování:
     • Žárovka svítí (Y = 1) v těchto případech:
       • A = 0, B = 0, C = 1
       • A = 0, B = 1, C = 0
       • A = 0, B = 1, C = 1
       • A = 1, B = 0, C = 1
       • A = 1, B = 1, C = 0
     • Žárovka nesvítí (Y = 0) v těchto případech:
       • A = 0, B = 0, C = 0
       • A = 1, B = 0, C = 0
       • A = 1, B = 1, C = 1

Sestavní pravdivostní tabulky a logické funkce na základě analýzy